[9465] 스티커 - C++

 

이 글은 정말 이해가 가지 않는 분들을 위해 쓰인 글입니다.

---

문제

브루트 포스를 생각할 수 도 있지만 $ O(2^n) $이며 입력의 최대 값이 100'000만 인 것을 보아 불가능하다.

 

Q. 과연 DP로는 풀 수 있을까?

A. DP [i] = i번째 까지 스티커를 떼었을 때의 최댓값으로 놓고 푼다면 가능하다.

 

경우의 수들이 존재하는데 그림으로 보자

 

i번째 스티커를 떼기 위한 경우의 수들

떼려는 스티커 = 파란색

파란색을 뗴기 위한 전까지의 최댓값 = 주황색

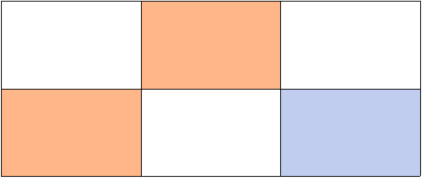
위 그림처럼 4가지 존재하며 이것을 구현해 주면 된다.

 

코드

#include <bits/stdc++.h>

using namespace std;
void init(){
  ios_base::sync_with_stdio(false);
  cin.tie(0);
  cout.tie(0);
}

int t, n;
int dp[2][100'002];

int main(){
  init();
  cin >> t;
  
  while(t--){
    cin >> n;
    for(int i=0; i < 2; ++i)
      for(int j = 1; j<=n; ++j)
        cin >> dp[i][j];
        
    dp[0][2] += dp[1][1];
    dp[1][2] += dp[0][1];
    
    for(int j = 3; j <= n; ++j){
      dp[0][j] += max(dp[1][j-2], dp[1][j-1]);
      dp[1][j] += max(dp[0][j-2], dp[0][j-1]);
    }
    
    cout << max(dp[0][n], dp[1][n]) << '\n';
  }
  return 0;
}

 

분석

dp[0][2] += dp[1][1];
dp[1][2] += dp[0][1];

왠지 이 부분이 의아했을 것 같다.

첫 번째는 무조건 떼어내며 진행하기에 2번째 까지는 미리 지정하고 가는 것이다.

---

글을 마무리하며

쉽지 않은 문제다, 그렇다고 이 문제만 보고 어렵다며 포기한다면 당신은 성장할 수 없을 것이다.

어려워도 계속 도전하는 당신이 되었으면 좋겠다.

나의 성장이 멈춘다는 것만큼 절망 적인 것이 있을까.

 

언제나 어려울 당신과 나를 위해 이 글을 쓴다.